In the fable "The frog and the ox" by Aesop, a frog tries to appear bigger than it actually is by inflating itself more and more...till it bursts. Well, that's not the end of the story, but the frog's behaviour resembles a bit what Facebook has done with one of its metrics: the average time people stay in front of a video. This metric is a key for prospective ad space buyers, since it is a proxy for the average exposure of Facebook users to ads: the longer the exposure, the higher the value of the advertising space. The metric is particularly important for a company like Facebook, whose product is basically you and your time. The news broke after the advertising company Publicis warned its customers about the alleged miscalculation by Facebook, and was reported by the Wall Street Journal. Facebook itself admitted the "discrepancy" by posting a clarification note on the computation method.
In the fable "The frog and the ox" by Aesop, a frog tries to appear bigger than it actually is by inflating itself more and more...till it bursts. Well, that's not the end of the story, but the frog's behaviour resembles a bit what Facebook has done with one of its metrics: the average time people stay in front of a video. This metric is a key for prospective ad space buyers, since it is a proxy for the average exposure of Facebook users to ads: the longer the exposure, the higher the value of the advertising space. The metric is particularly important for a company like Facebook, whose product is basically you and your time. The news broke after the advertising company Publicis warned its customers about the alleged miscalculation by Facebook, and was reported by the Wall Street Journal. Facebook itself admitted the "discrepancy" by posting a clarification note on the computation method.
But what is then the true average time people stay in front of a video on Facebook? The true value appears to be private to Facebook, which releases it to its prospective customers. We can however gain some insight through some very simple calculations.
We know that Facebook censored data by neglecting watching times shorter than 3 seconds. In order to see the impact of censoring on the average watching time, we must assume a probability distribution for watching time. If we assume that the watching time 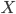 follows an exponential distribution (though this seems to imply that videos can be watched for an infinite time, it serves just as a model since the probability of watching time exceeding a physically feasible value can be extremely small), the average watching time
follows an exponential distribution (though this seems to imply that videos can be watched for an infinite time, it serves just as a model since the probability of watching time exceeding a physically feasible value can be extremely small), the average watching time ![\mathbb{E}[\hat{X}]](http://www.maurizionaldi.it/wp-content/plugins/latex/cache/tex_dd6de14d72d69a59d4d2454a2746b657.gif) computed after censoring durations shorter than 3 seconds is, quite simply, the true average
computed after censoring durations shorter than 3 seconds is, quite simply, the true average ![\mathbb{E}[X]](http://www.maurizionaldi.it/wp-content/plugins/latex/cache/tex_6b4b92dccdc1aba0add8de19bc101e9c.gif) value plus 3 seconds.
value plus 3 seconds.
![\mathbb{E}[\hat{X}] = \mathbb{E}[X]+3](http://www.maurizionaldi.it/wp-content/plugins/latex/cache/tex_8949ef5b70ce5cdaa5c15d7f636e82ff.gif)
Publicis itself reported that the miscomputation led to inflating the average watching time by 60 to 80%, i.e.
![1.6 \cdot\mathbb{E}[X] < \mathbb{E}[\hat{X}] < 1.8 \cdot\mathbb{E}[\hat{X}]](http://www.maurizionaldi.it/wp-content/plugins/latex/cache/tex_4c82d683ad650ebb3a61633c9921482a.gif)
Putting the two pieces of information together and doing the math, we find that the true average watching time is between 3.75 and 5 seconds (but is mistakenly reported as lying between 6.75 and 8 seconds), quite small, maybe a bit too small for prospective ad buyers...